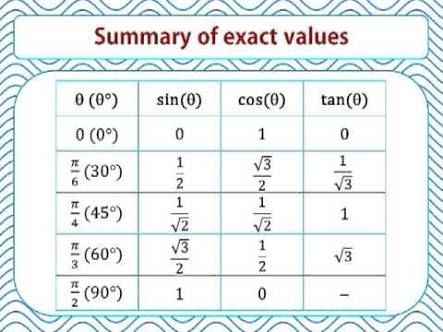
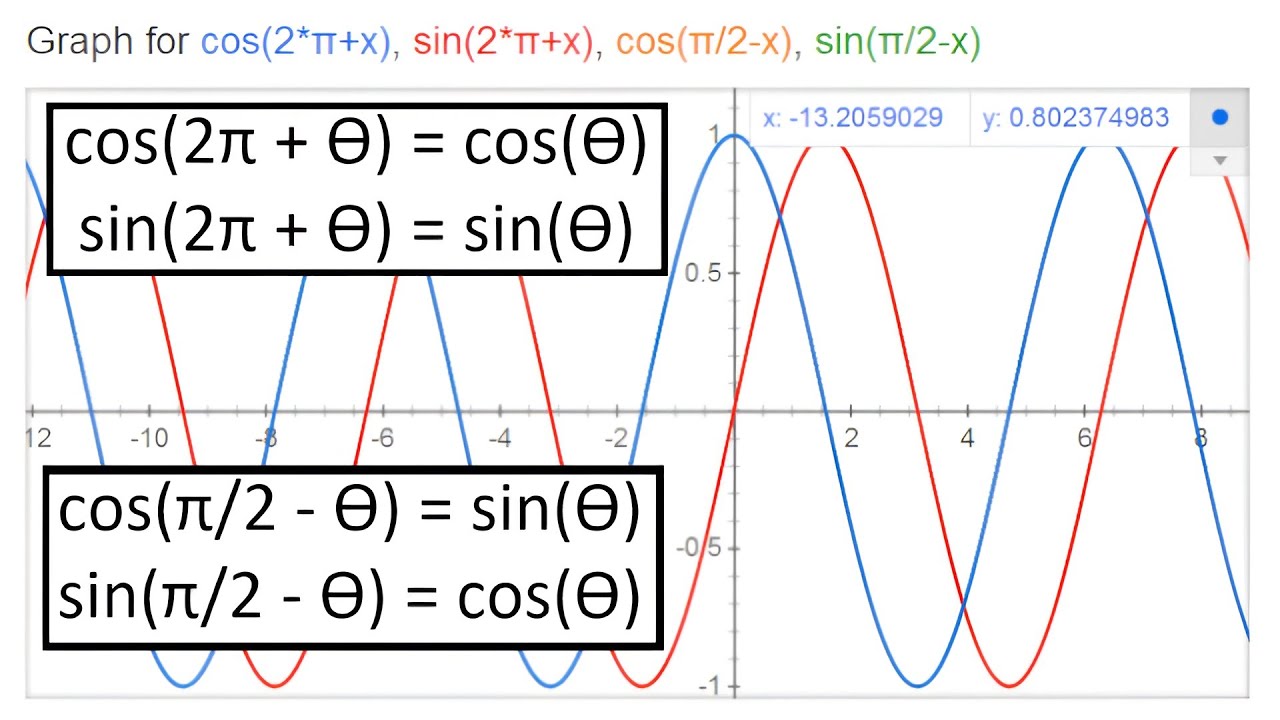
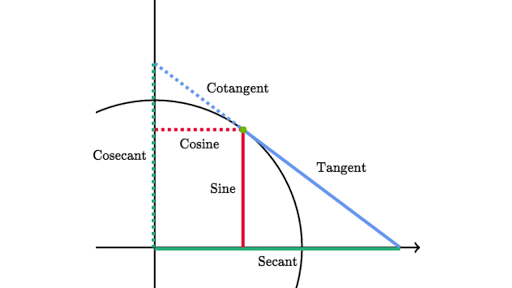
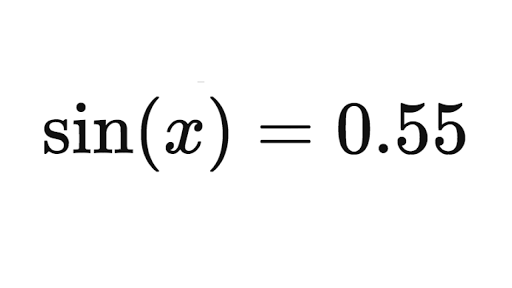Formula Of Cos Pi Minus Theta

Here we will find the relation between all trigonometrical ratios.

Formula of cos pi minus theta. While right angled triangle definitions allows for the definition of the trigonometric functions for angles between 0 and radian 90 the unit circle definitions allow. A formula for computing the trigonometric identities for the one third angle exists but it requires finding the zeroes of the cubic equation 4x 3 3x d 0 where x is the value of the cosine function at the one third angle and d is the known value of the cosine function at the full angle. θ means starting from a the origin on the unit circle and just going clockwise negative direction as much as θ. The six trigonometric functions can be defined as coordinate values of points on the euclidean plane that are related to the unit circle which is the circle of radius one centered at the origin o of this coordinate system.

For example if you are on the terrace of a tall building of known height and you see a post box on the other side of the road you can easily. To find the second solution subtract the reference angle from to find the solution in the fourth quadrant. Let a ray ox revolve anti clockwise direction to make an angle angle xoa theta. Thinking of θ as an acute angle θ ends in the 4th quadrant where only cosine is positive.

Trigonometry is the branch of mathematics that deals with the relationship between the sides and angles of a triangle. In this section we will discuss the relation among all trigonometric ratios of minus theta θ.